进位制
# 进位计数制
# 任意进制转十进制
#
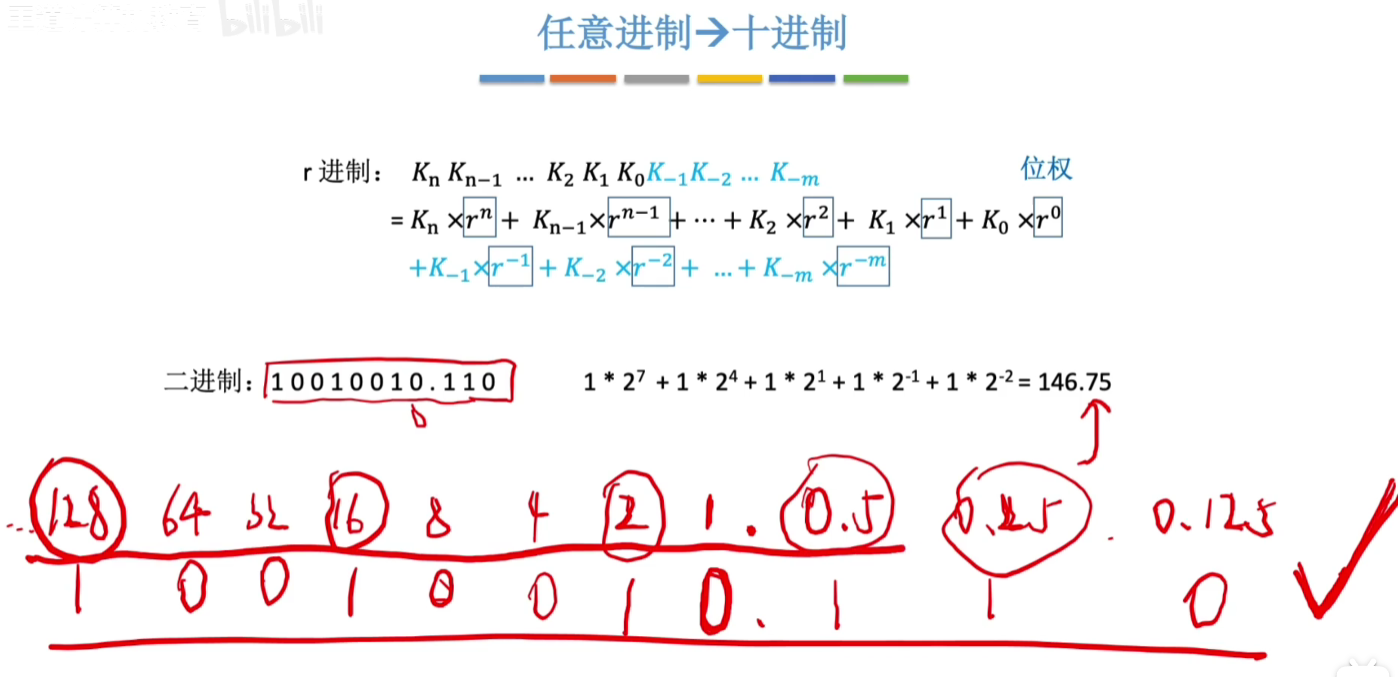
# 二进制转八进制/十六进制
# 十六进制/八进制转二进制
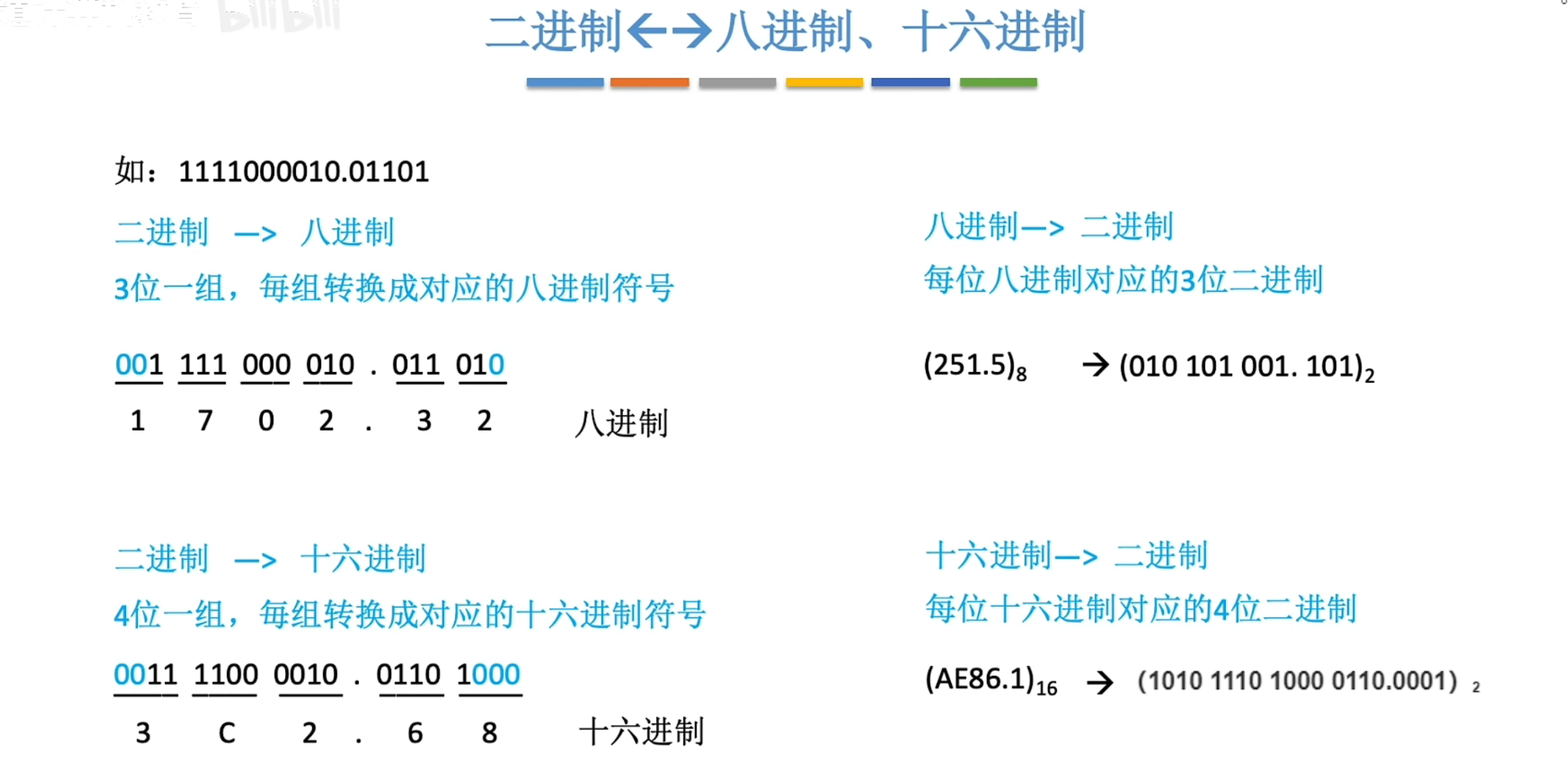
# 十进制转任意进制
# 总结
# 补位
整数部分进行高位补位，小数部分进行低位补位
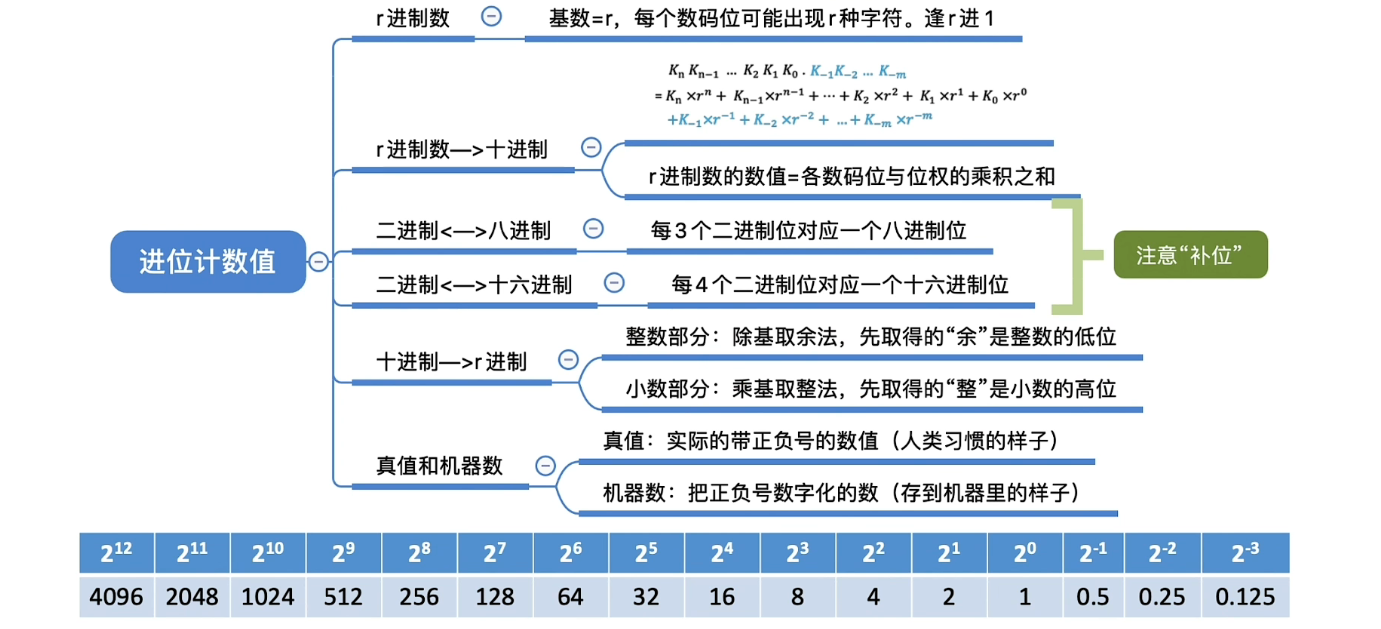
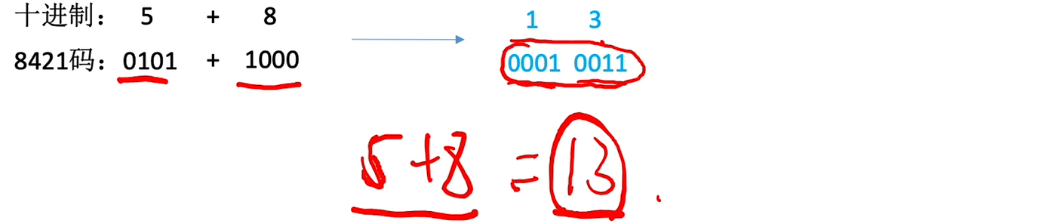
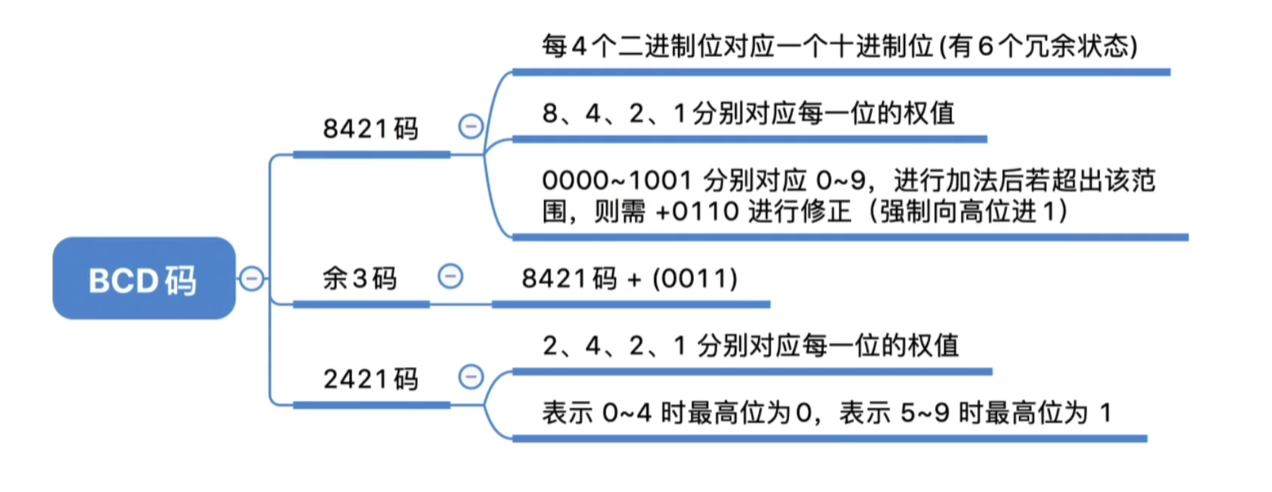
# BCD码
8421码、余3码、2421码
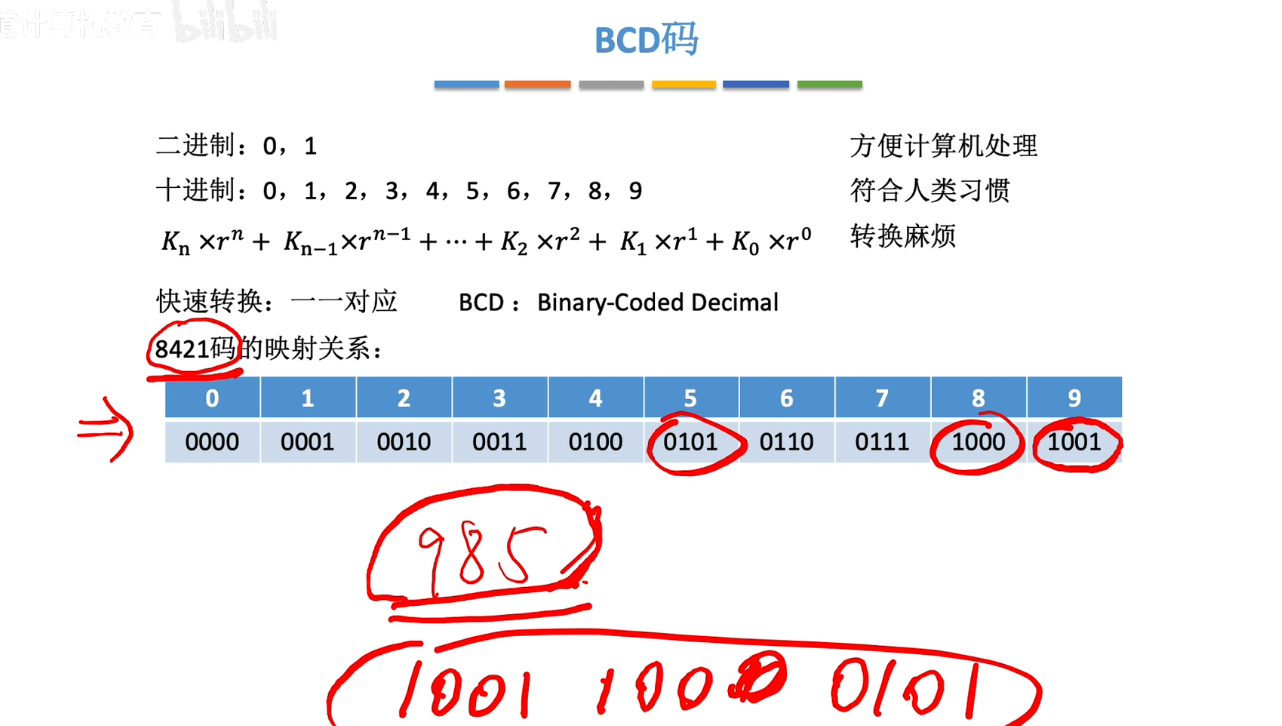
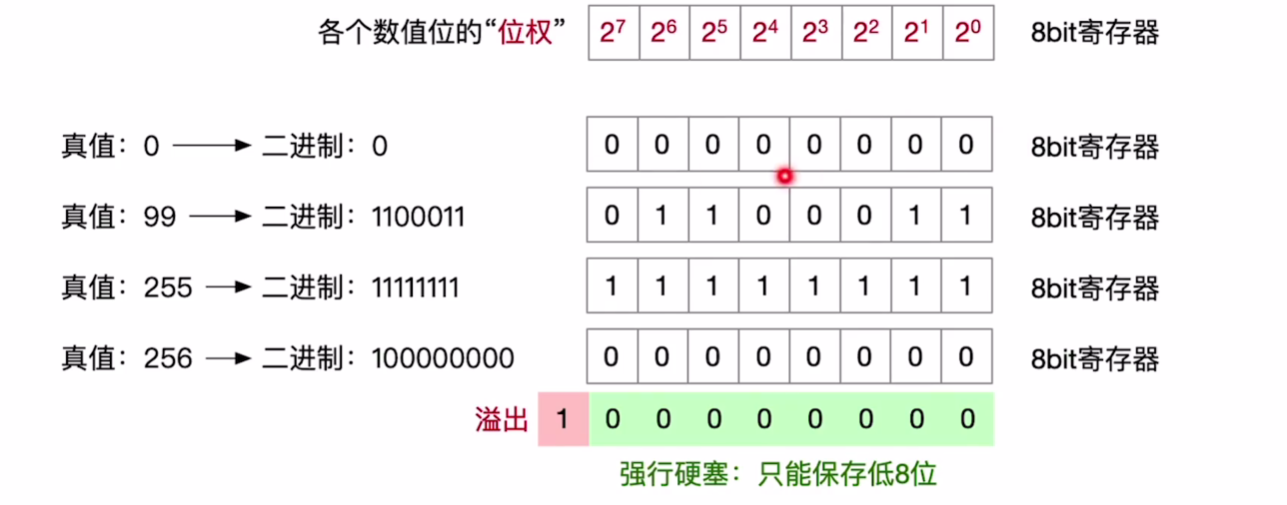
# 无符号整数
# 无符号加法
从低位开始，按位相加，并往更高位进位
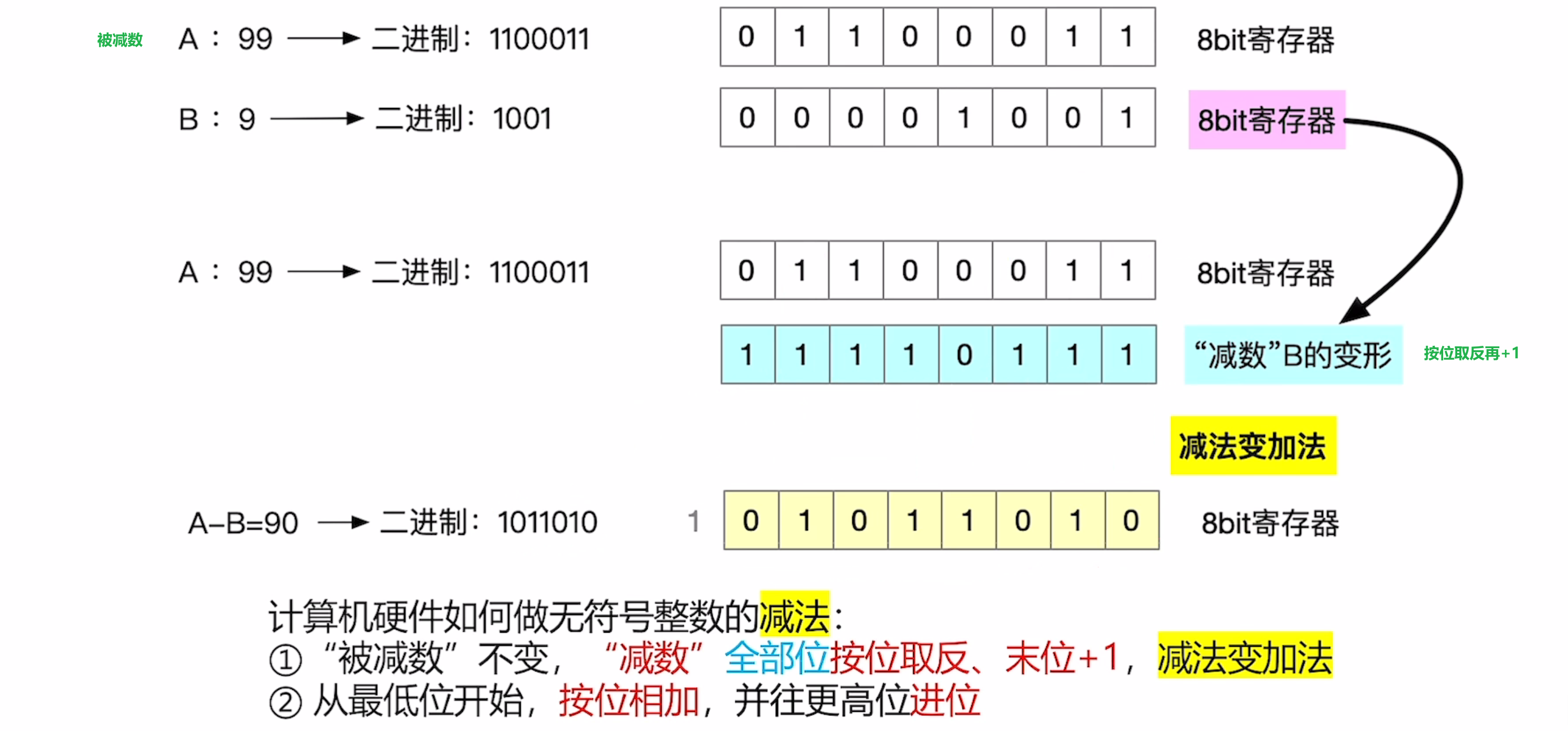
# 无符号减法
1."被减数"不变，“减数”全部位按位取反、末位+1，减法变加法
2.从最低位开始，按位相加，并往更高位进位
# 带符号整数（表示和运算）
（原/反/补）
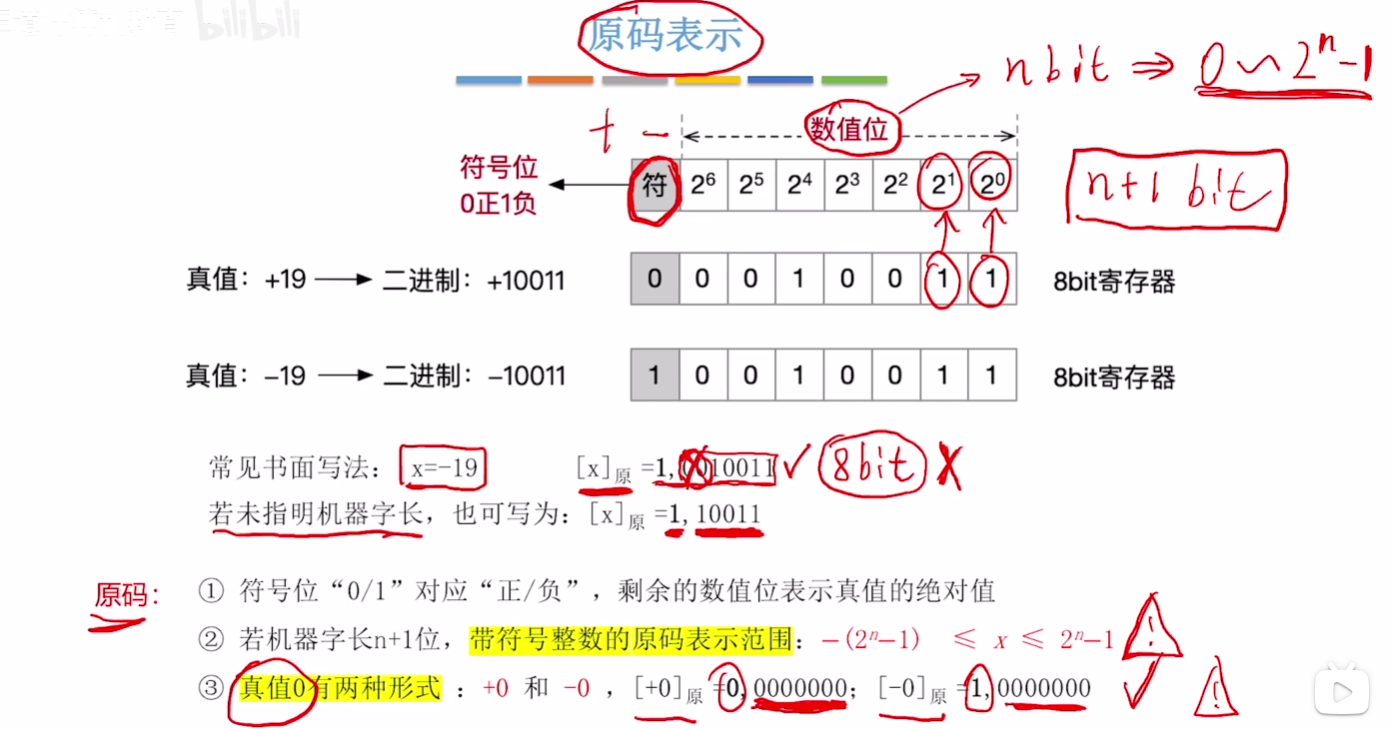
# 原码表示
原码缺点：符号位不能参与运算，需要设计复杂的硬件电路
# 运算
用补码表示真值——符号位可以参与运算
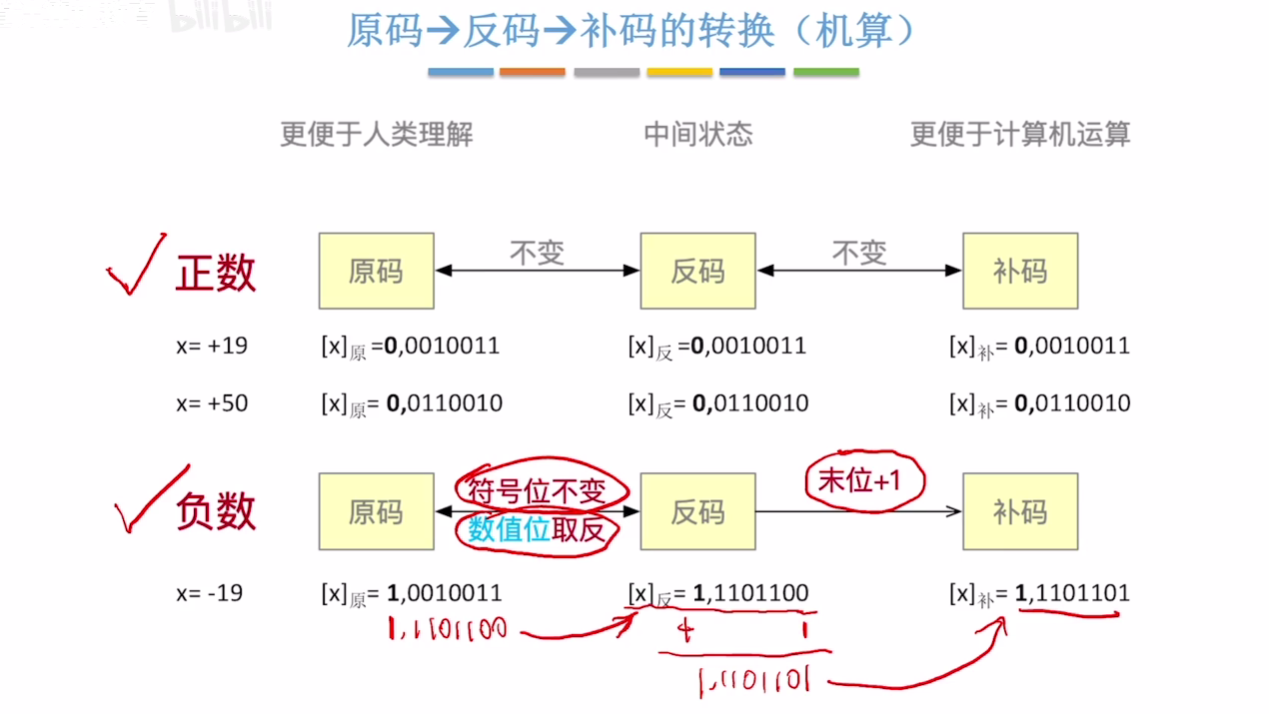
# 机算
原码-->反码：符号位不变、数值位取反
反码-->补码：末位+1
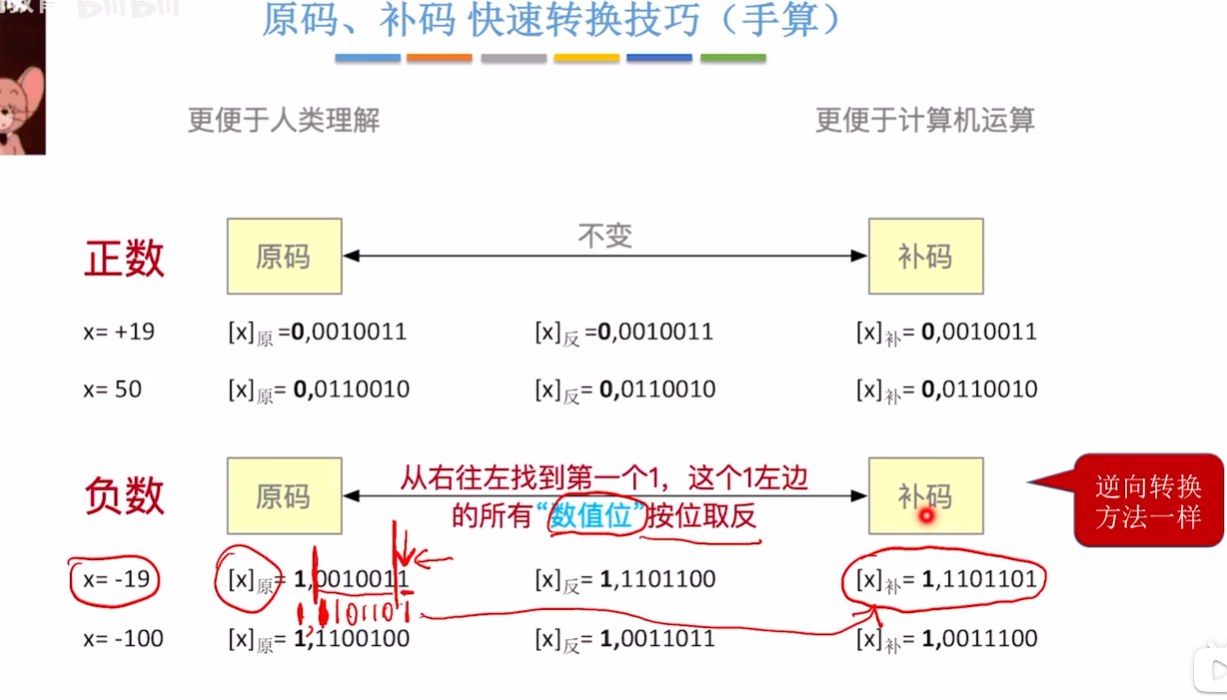
# 快速技巧（手算）
原码-->补码：从右往左找到第一个1，这个1左边的所有“数值位”按位取反
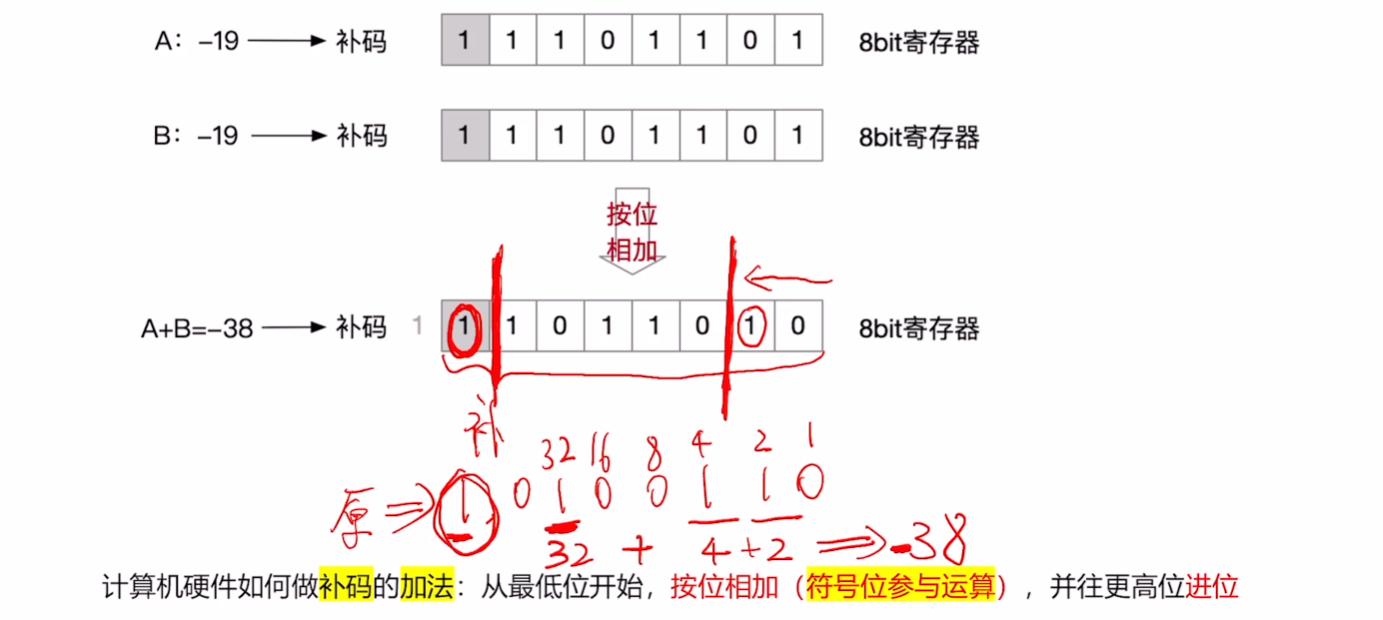
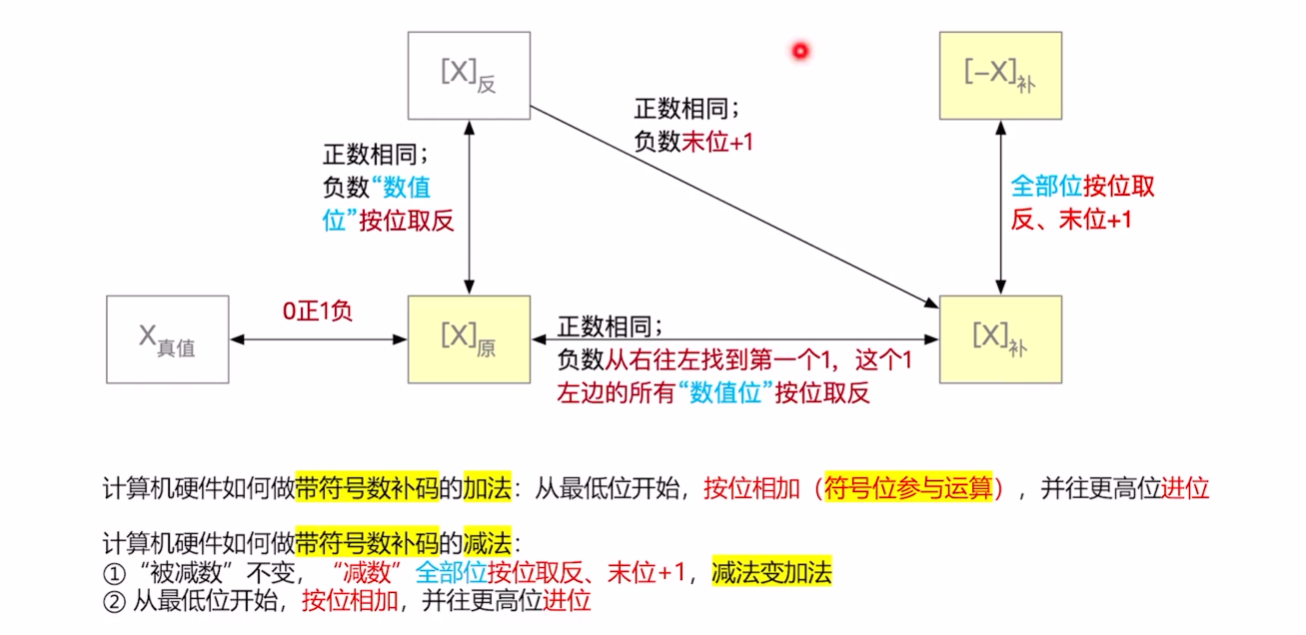
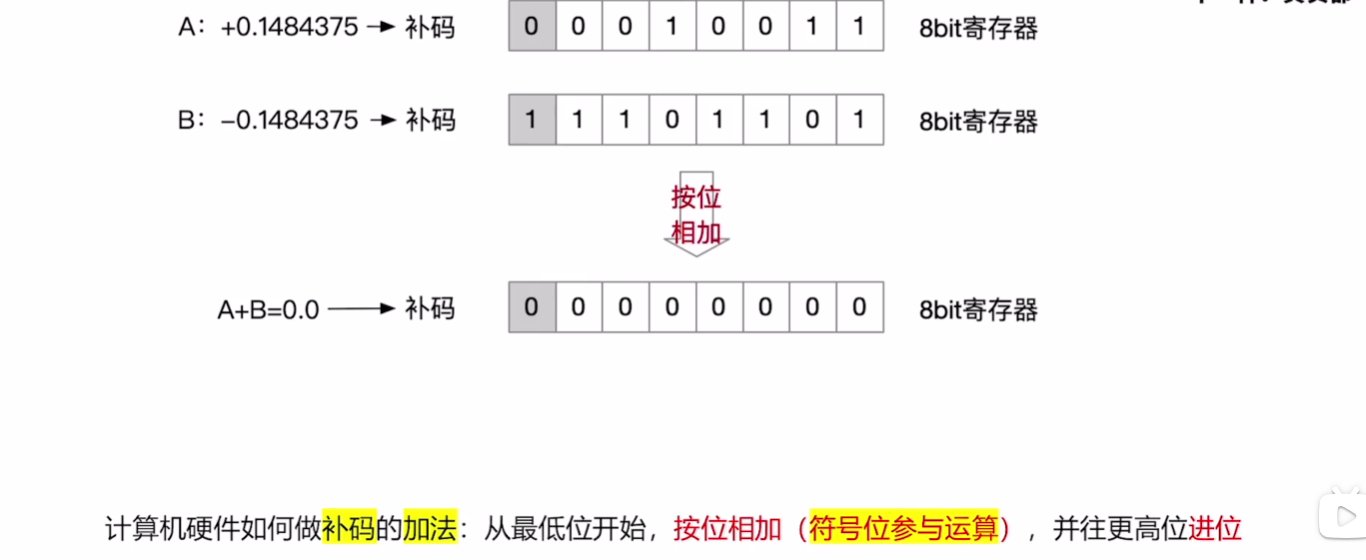
# 补码的加法
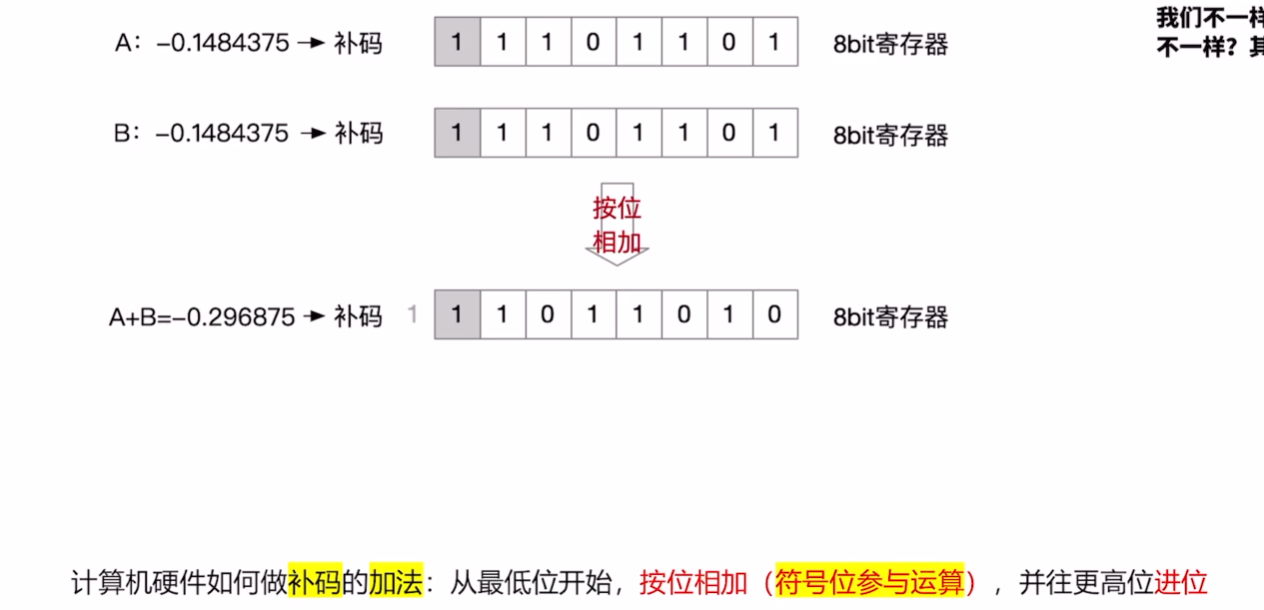
计算机硬件如何做补码的加法：从最低位开始，按位相加（符号位参与运算），并往更高位进位
# 例子1
补码后
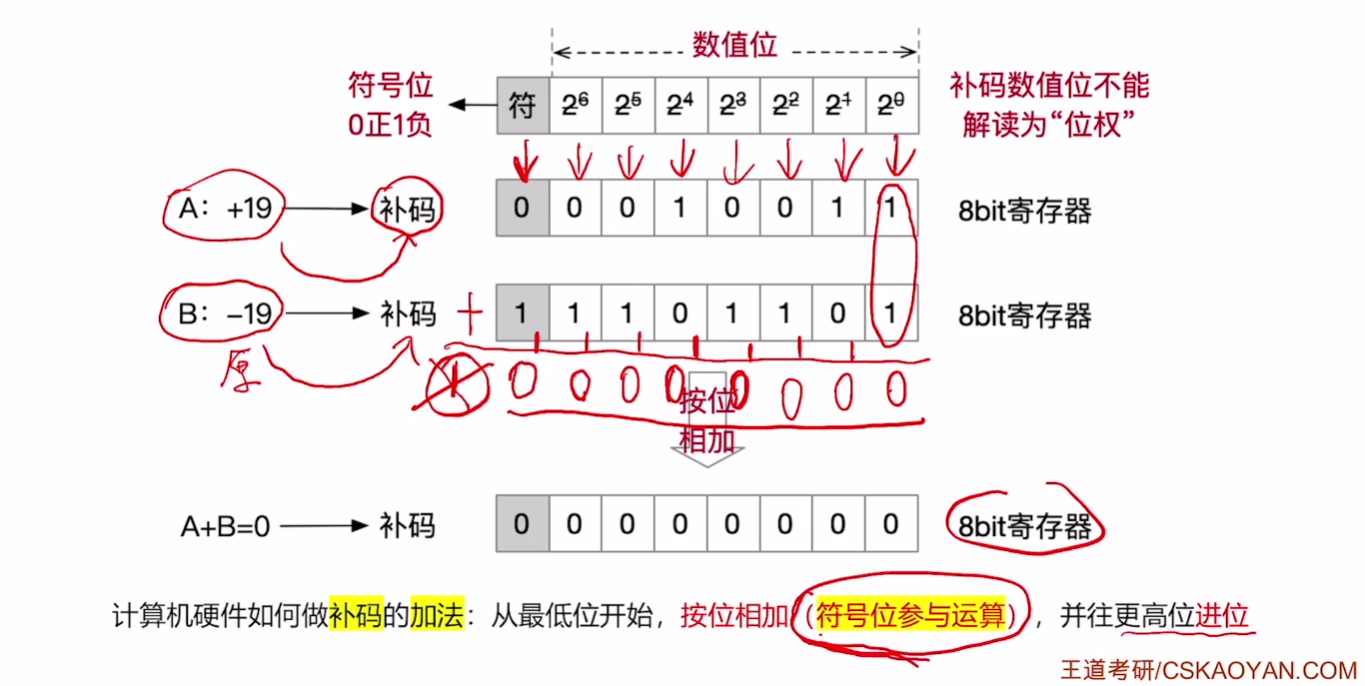
补码表示数值，对于负数来说，直接看不出真值是多少，需将补码转换成原码，再去解读真值
# 例子2
补码后
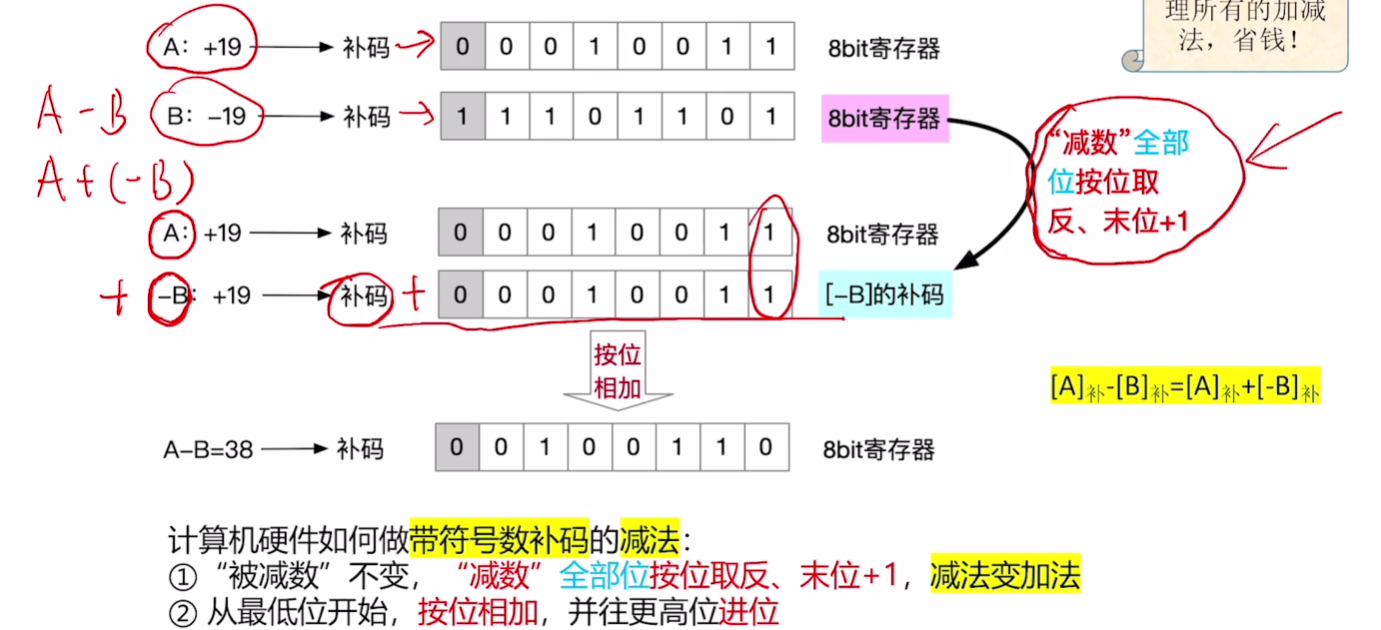
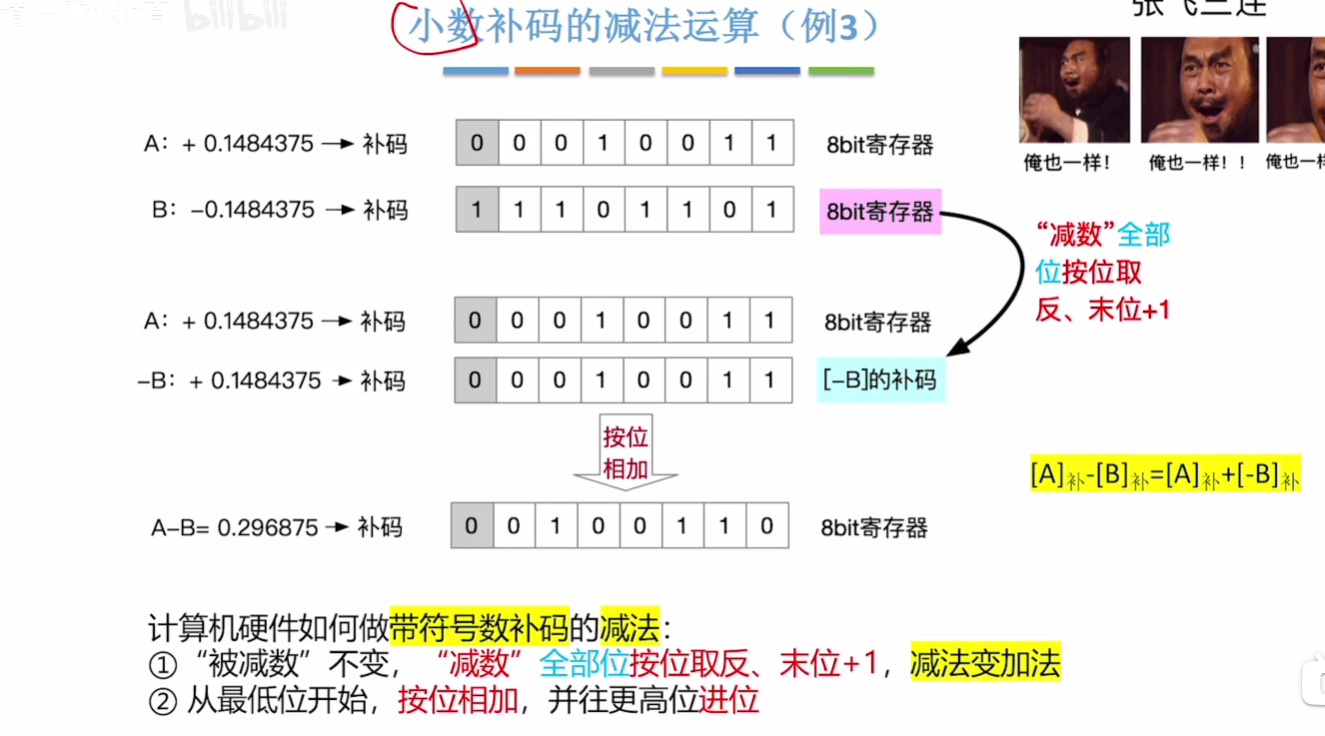
# 补码的减法
考虑加法电路造价便宜，减法电路造价昂贵
[A]补-[B]补 = ？ ==> A+(-B)
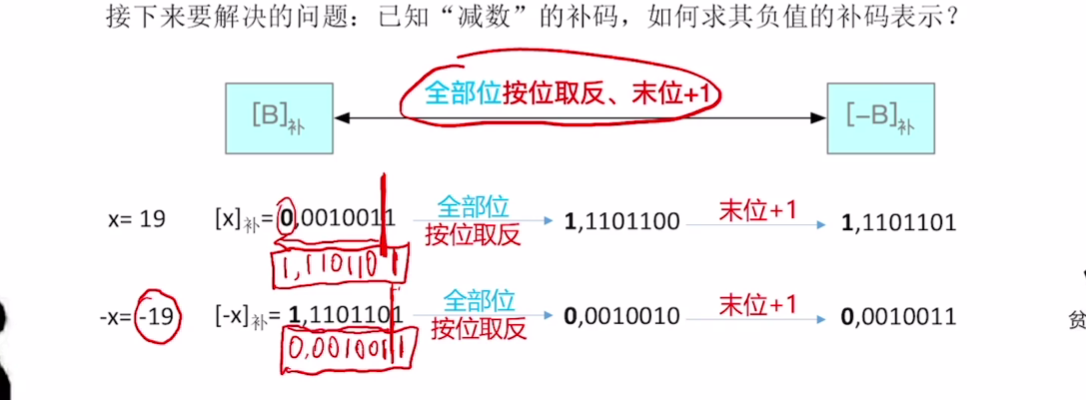
[B]补-->[-B]补： 全部位（包括符号位）按位取反、末位+1 / 从右往左找到第一个1，这个1左边的所有位（包括符号位）按位取反
# 例子3
与无符号整数减法一致
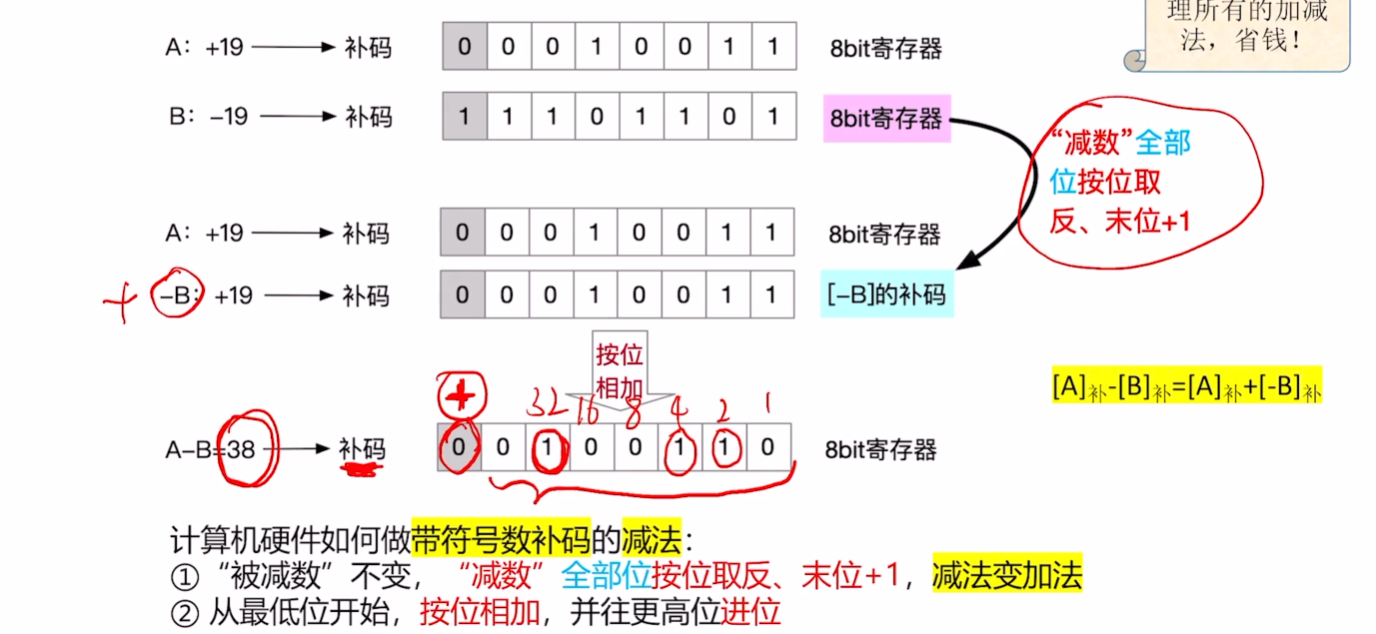
# 总结
有符号整数的补码减法和无符号整数的剑法方法一样，只需要用同一套电路即可实现
计算机内部，所有带符号证书的加、减法都要先转化为补码
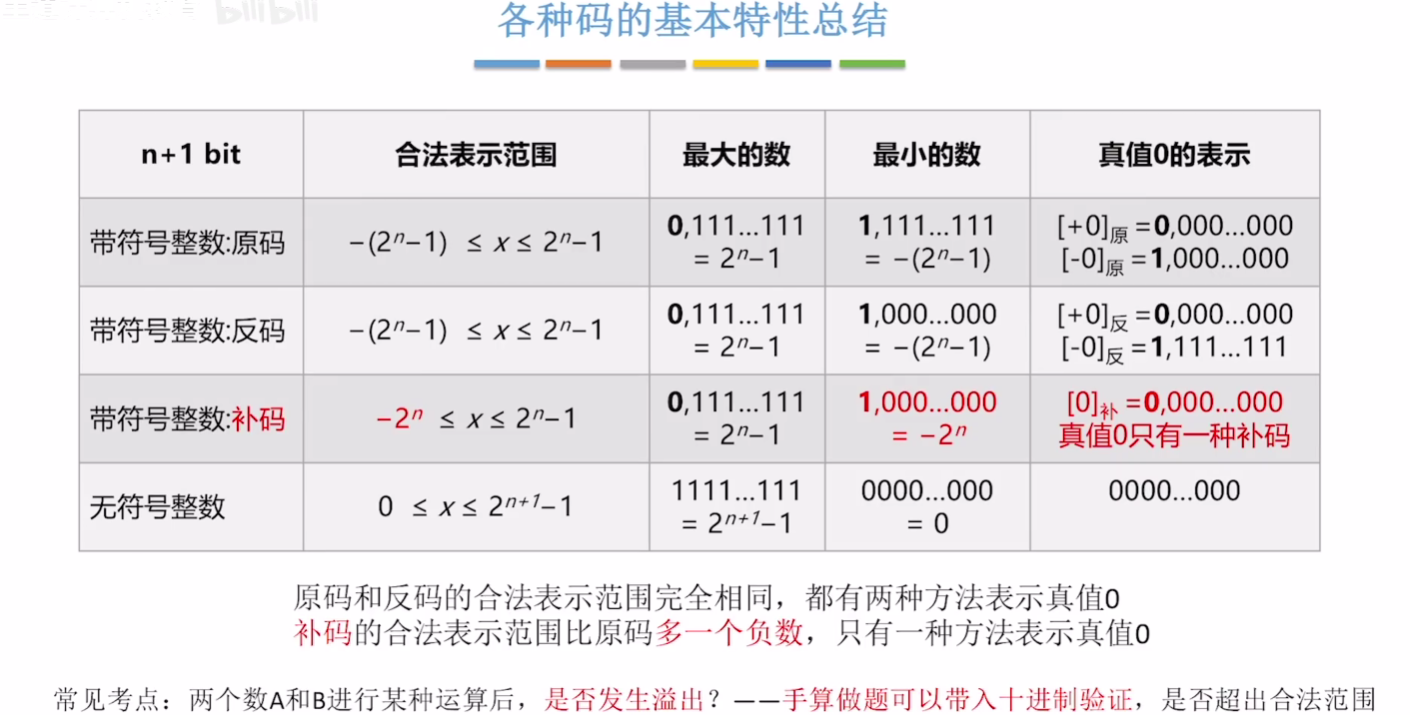
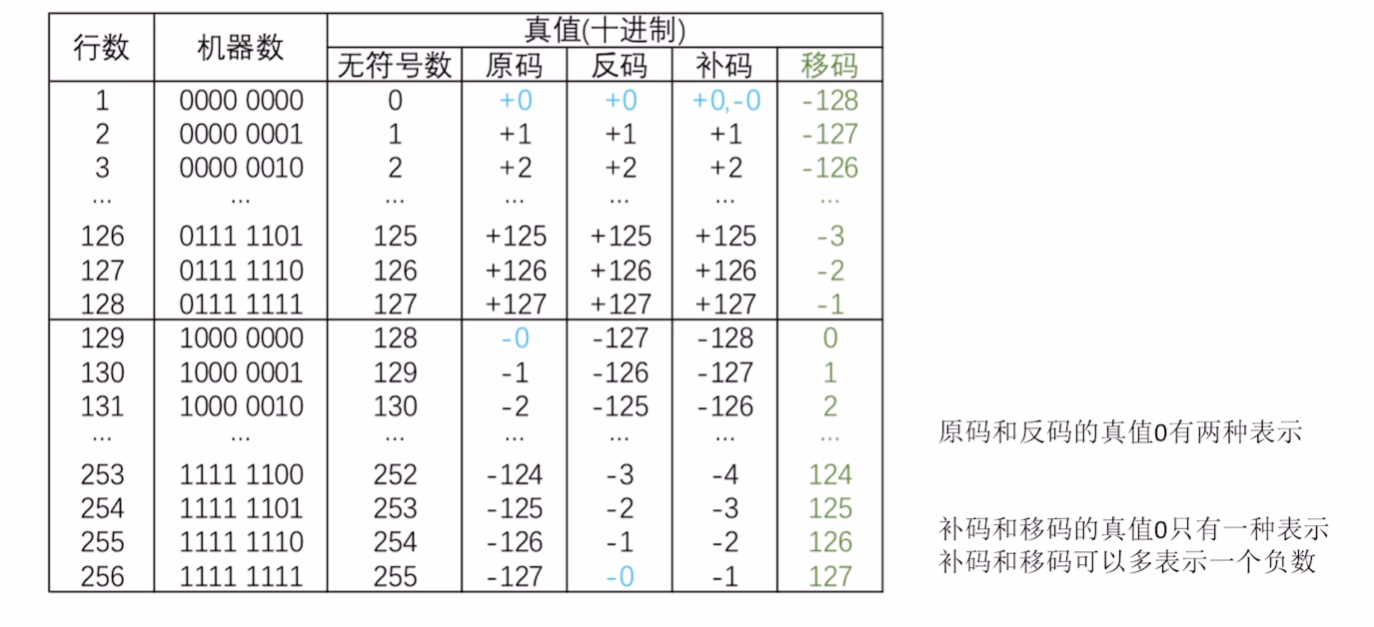
# 原/反/补码 特性对比
# 前言
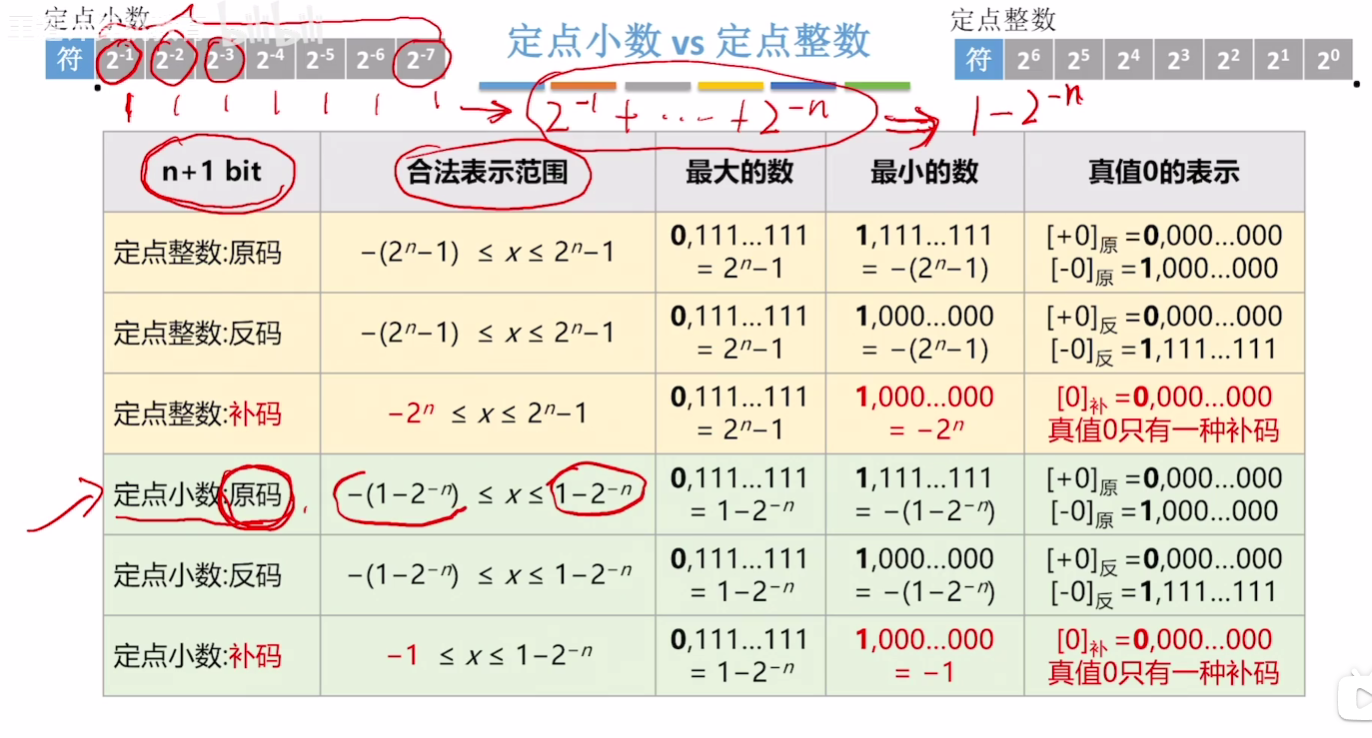
- n+1 bit的合法表示范围
- 最大的数怎么表示、最小的数怎么表示
- 真值0的表示
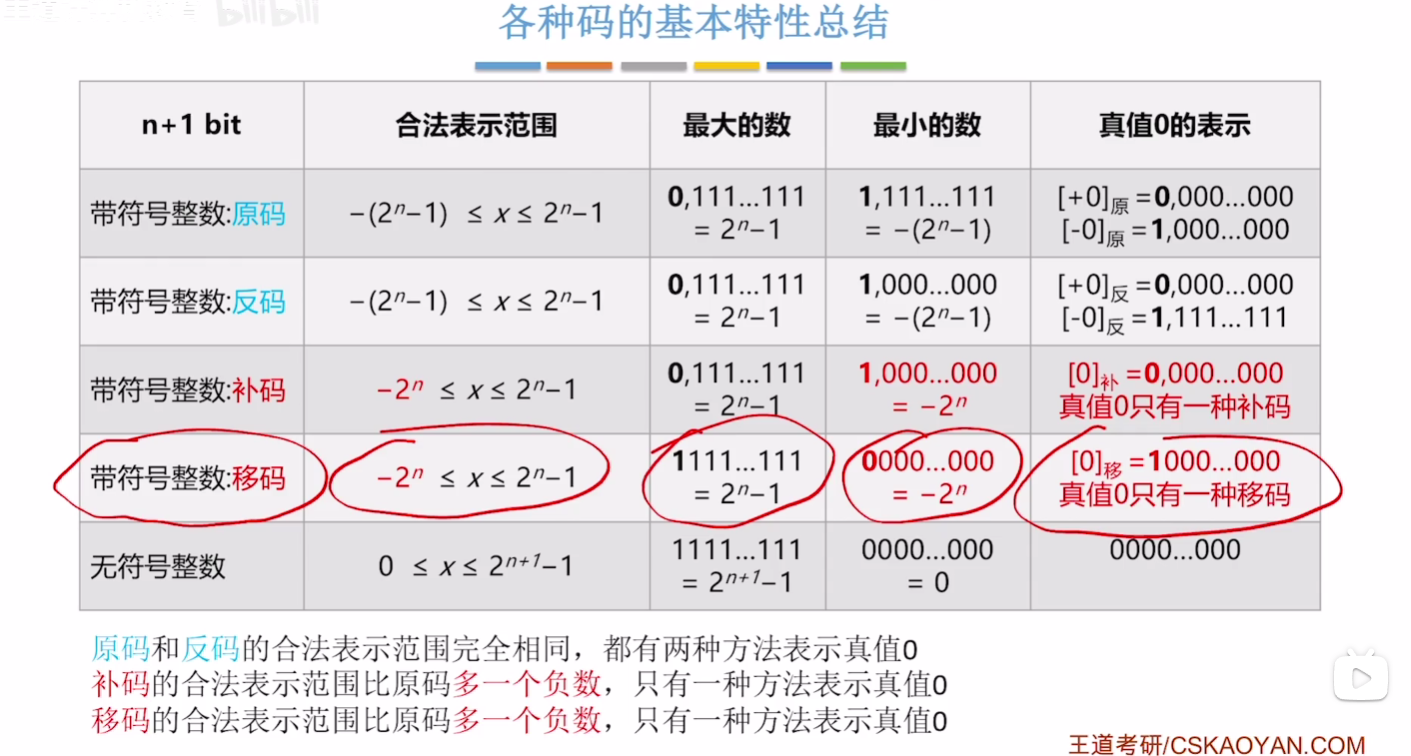
# 原、反、补、移码的转换
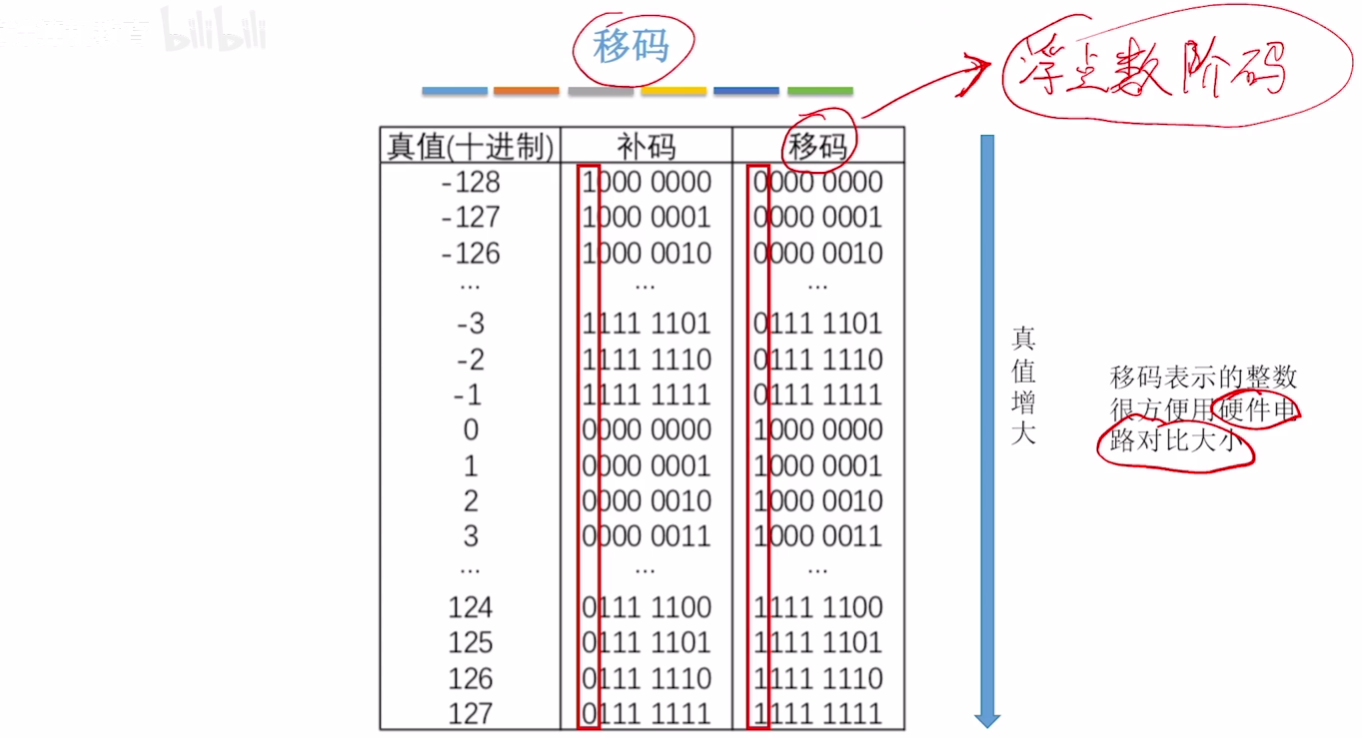
移码：补码符号位取反
# 移码
# 定点小数
定点整数——带符号整数
定点小数
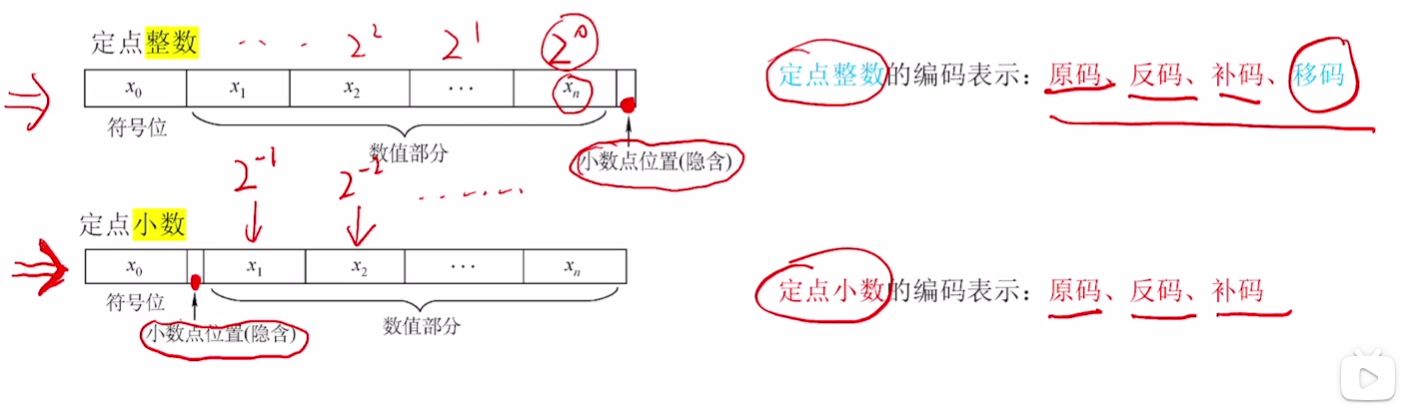
两者相比位权不一致
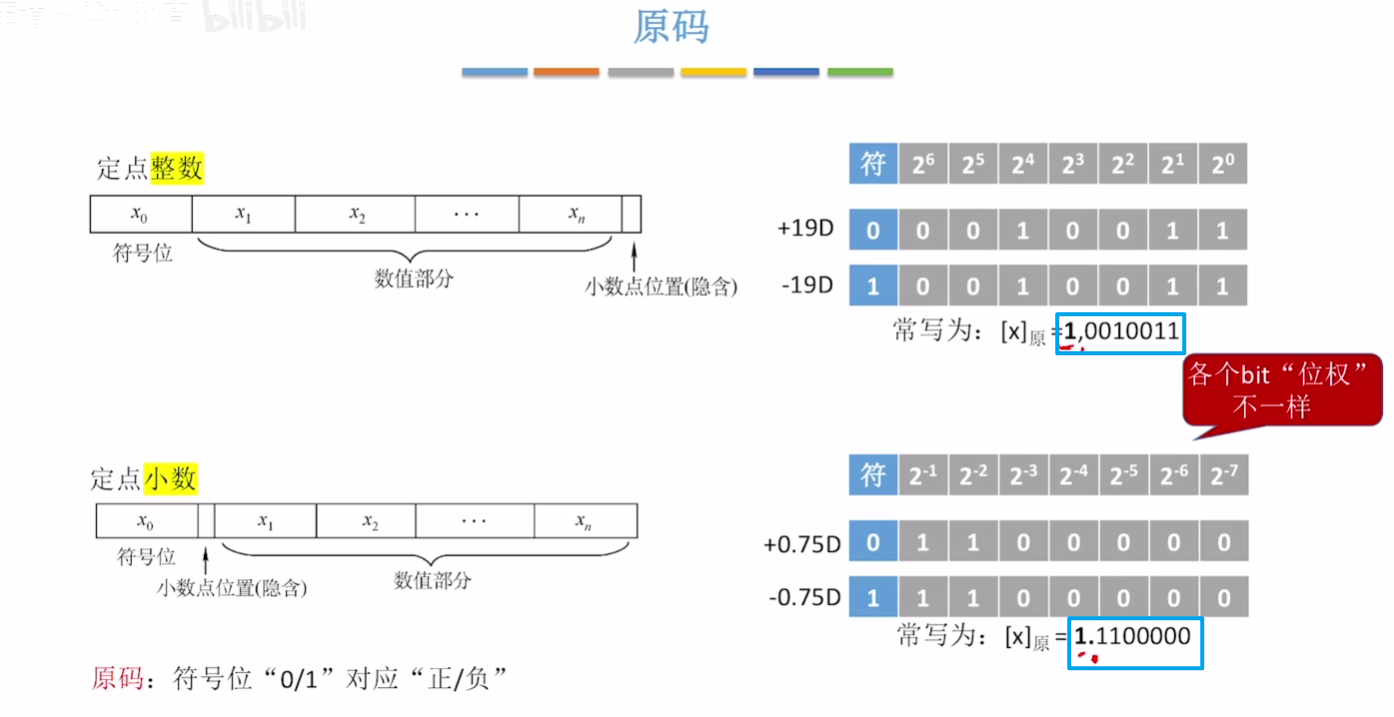
原、反、补、移码的转换与定点整数一样
# 定点小数加减运算
与定点整数一样
# 
例子1
# 奇偶校验
上次更新: 2024/08/14, 04:14:33